Jupyter Test

08 Mar 2017

This is a Jekyll-Jupyter test

Here I will betesting the functionality of using Jupyter to create a Jekyll blog post

#These are all the things I import
%matplotlib inline
from IPython.core.pylabtools import figsize
import numpy as np
from matplotlib import pyplot as plt
figsize(11, 9)

import scipy.stats as stats
import pandas as pd
import pymc3 as pm

/Users/Sean/Dropbox/.virtualenvs/bayes_python/lib/python3.5/site-packages/matplotlib/__init__.py:913: UserWarning: axes.color_cycle is deprecated and replaced with axes.prop_cycle; please use the latter.
  warnings.warn(self.msg_depr % (key, alt_key))

Import the data

We’re going to use the “Iris” data set (reference blah blah)

iris = pd.read_csv("iris.csv")
iris = iris.loc[iris["Species"] != "setosa"]

Looking at the data

Here are some plots. WEEEEEE!

colours = ["#348ABD", "#A60628"]
spec = iris.Species.unique()

figsize(12.5, 4)
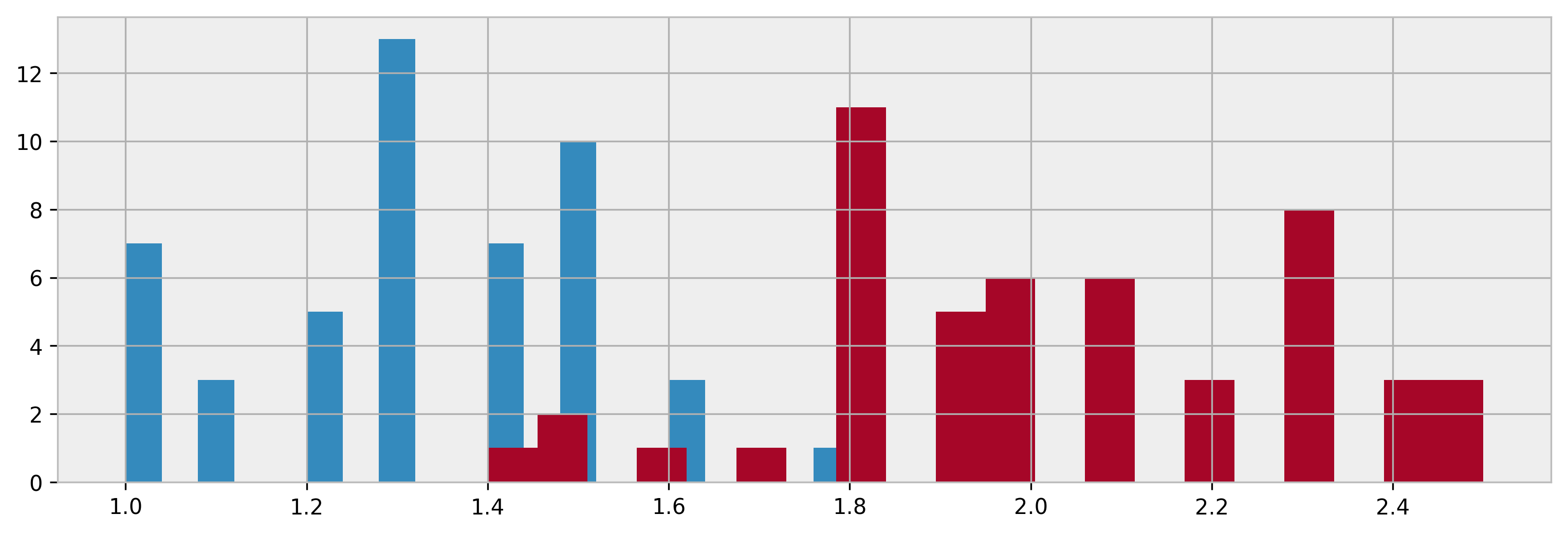
plt.hist(iris.loc[iris["Species"]==spec[0],"Petal.Width"],20,color=colours[0])
plt.hist(iris.loc[iris["Species"]==spec[1],"Petal.Width"],20,color=colours[1])

png

Bayesian MCMC

Here is a big old PyMC3 model

# From "https://pymc-devs.github.io/pymc3/notebooks/BEST.html" with special thanks to Kruschke

# Likelihood functions
## y_group_i ~ T(v,mu_i,sig_i) <- v=degrees of freedom, mu=mean, sig=variance, T=t-distribution

## SETTING PRIORS FOR MEANS##
# Means are real valued and thus normally distributed

mu_prior = iris["Petal.Width"].mean() # Use grand mean as starting value
s_prior = iris["Petal.Width"].std() * 2 # Use 2*SD as starting value

with pm.Model() as model:
    group1_mu = pm.Normal('group1_mu',mu_prior,sd=s_prior) # Hypothetical distribution for group1 mean
    group2_mu = pm.Normal('group2_mu',mu_prior,sd=s_prior)

## SETTING PRIORS FOR SD ###
sig_low = iris["Petal.Width"].std() / 10
sig_high = iris["Petal.Width"].std() * 10

with model:
    group1_sd = pm.Uniform('group1_sd',lower=sig_low,upper=sig_high)
    group2_sd = pm.Uniform('group2_sd',lower=sig_low,upper=sig_high)

## SETTING PRIORS FOR DF ###

with model:
    v = pm.Exponential('v_minus_one',1/29.) + 1

## PARAMATERIZE STUDENTS T ##
# Parameterize T with precision, not variance
with model:
    lam_1 = group1_sd**-2
    lam_2 = group2_sd**-2

    group1 = pm.StudentT('versicolor', nu=v, mu=group1_mu, lam=lam_1, observed=iris.loc[iris["Species"]==spec[0],"Petal.Width"])
    group2 = pm.StudentT('virginica', nu=v, mu=group2_mu, lam=lam_2, observed=iris.loc[iris["Species"]==spec[1],"Petal.Width"])


## ESTIMATE DIFFERENCES ##
with model:
    diff_of_means = pm.Deterministic('difference of means',group1_mu - group2_mu)
    diff_of_SDs = pm.Deterministic('difference of SDs', group1_sd - group2_sd)
    effect_size = pm.Deterministic('effect size',diff_of_means / np.sqrt((group1_sd**2 + group2_sd**2)/2))

## FIT THE MODEL ##
with model:
    #start = pm.find_MAP()
    #step = pm.METROPOLIS()
    #trace = pm.sample(4000, step=pm.Metropolis(), init=None, njobs=2)
    trace = pm.sample(8000,tune=1000)

Auto-assigning NUTS sampler...
Initializing NUTS using advi...
Average ELBO = -11.323: 100%|██████████| 200000/200000 [00:36<00:00, 5472.32it/s]
Finished [100%]: Average ELBO = -11.29
100%|██████████| 8000/8000 [00:19<00:00, 413.72it/s]

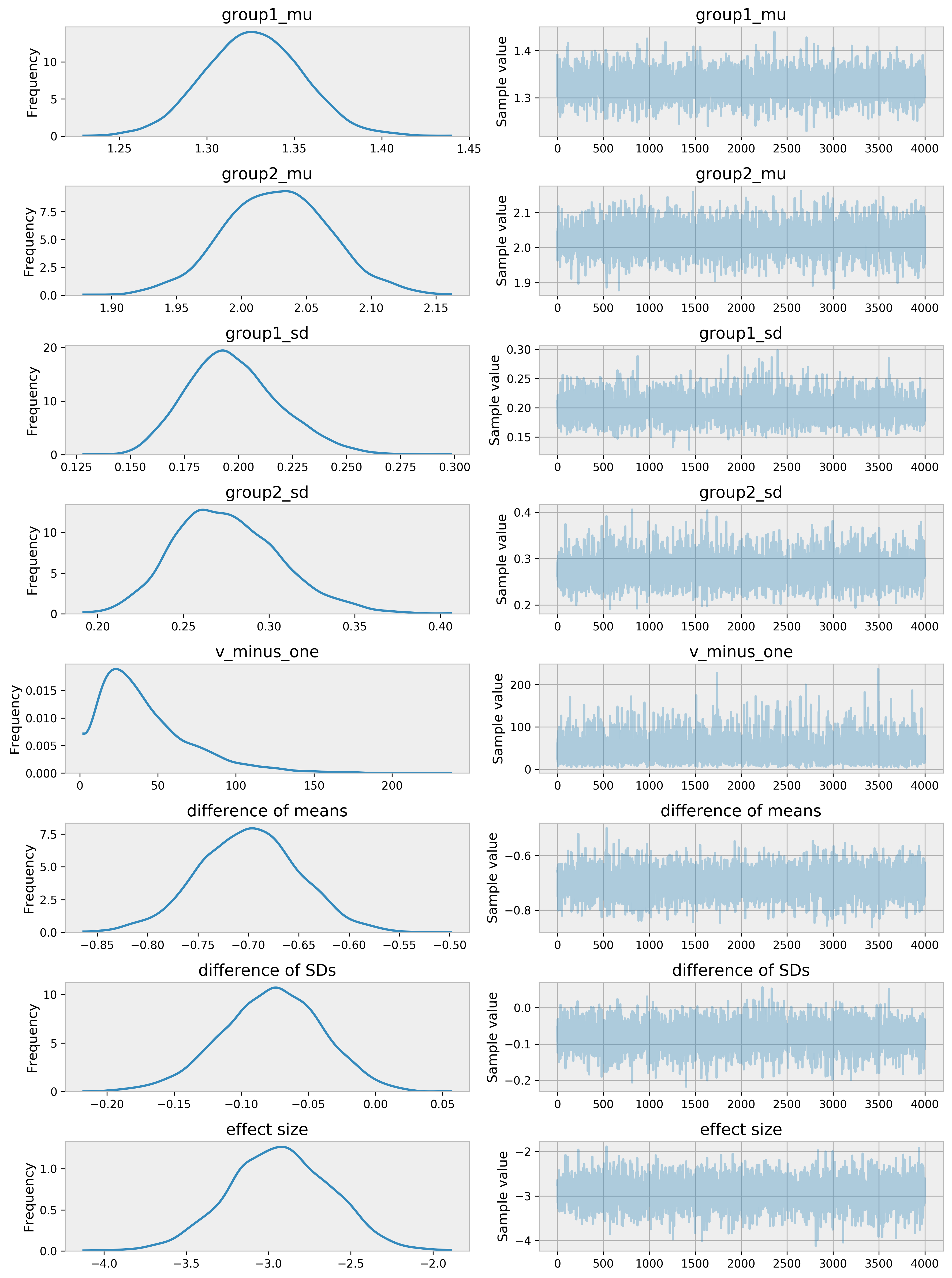
Final Plotting

Here is the trace evaluation plots

figsize(12.5,4)
pm.traceplot(trace[4000:])

png

Sean Linnaeus Barton